Understanding how we think and make decisions is an important skill. One key part is understanding different types of reasoning. Each type involves thinking in a specific way to make decisions.

In this article, we’ll explore the four main types of reasoning:

1. Inductive.
2. Deductive.
3. Abductive.
4. Analogical

By understanding these types, you can improve your thinking skills and make better choices in all areas of your life.

What are the 4 Types of Reasoning?

Deductive Reasoning

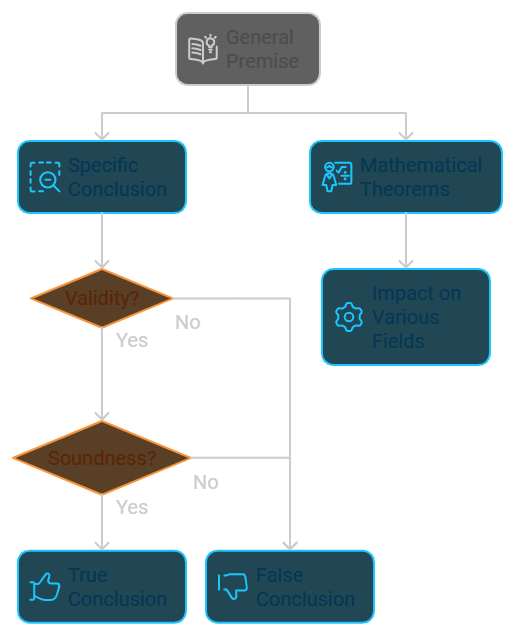
Deductive reasoning starts with a general rule or premise and then comes to a specific conclusion. It’s a structured process: the premise is the starting point, followed by applying the rule to specific cases, resulting in a particular conclusion.

To assess the validity and soundness of deductive reasoning, we look at whether the argument’s conclusion logically follows from the premises (validity) whether the argument is valid, and all the premises are true (soundness).

Famous examples of deductive reasoning include mathematical theorems. Logical rules are used to conclude by applying them to specific numbers or equations.

Inductive Reasoning

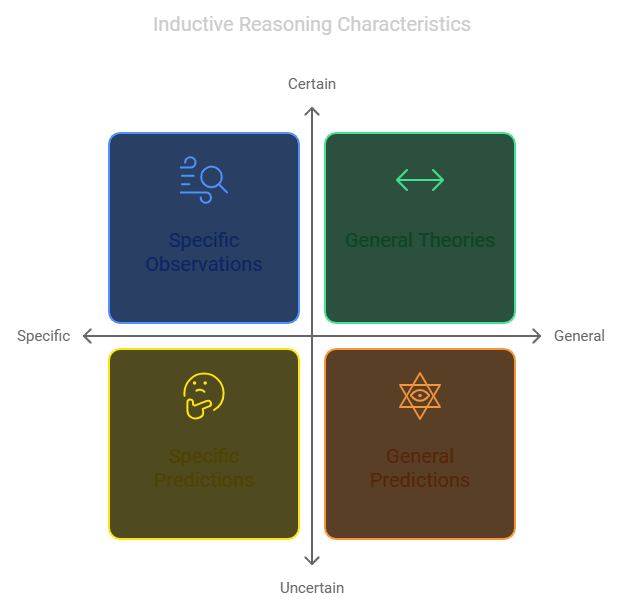
Inductive reasoning is when you make general conclusions from specific observations. Unlike deductive reasoning, it doesn’t guarantee complete certainty in its findings but establishes likelihood.

For example, if someone sees wet pavement every time they go outside, they might conclude that it has rained. This type of reasoning is helpful in scientific research for developing hypotheses and making predictions based on past observations. Unlike abductive reasoning, which starts with incomplete observations, inductive reasoning begins with specific observations and seeks to make broad generalizations. This method can increase our knowledge and understanding of the world. By understanding inductive reasoning, individuals can better grasp its role in scientific discoveries and problem-solving and discern its differences from other types of reasoning, like deductive and abductive reasoning.

Abductive Reasoning

Abductive reasoning starts with incomplete observations and arrives at the likeliest possible explanation. It is different from both deductive and inductive reasoning.

In scientific discovery, hypotheses are formed and educated guesses are made based on available data. People often use abductive reasoning to make decisions based on incomplete information, such as inferring a friend’s mood from their behavior.

Its strength lies in its creative and intuitive nature, allowing new ideas and theories to be generated. However, its limitations include a lack of certainty and the potential for multiple explanations to fit the available data, leading to potential biases or flawed conclusions.

In comparison, deductive reasoning guarantees a true conclusion if the premises are true, while inductive reasoning builds generalized conclusions from specific observations with uncertainty.

Analogical Reasoning

Analogical reasoning is a way of thinking that involves finding similarities between two different things. For example, it involves comparing a new technology to a familiar device to better understand it.

Analogies can also help innovation and learning by making complex ideas easier to understand. However, if differences are overlooked when comparing two similar situations, this may lead to wrong conclusions.

Even with its limitations, analogical reasoning is valuable in simplifying complex topics and is useful in many fields.

Deductive Reasoning Explored

Definition of Deductive Reasoning

Deductive reasoning is a conclusion based on a general rule or premise. You start with a general statement and then move to a specific one. The conclusion is true if the original statements are factual.

For example, “All men are mortal. Harold is a man. Therefore, Harold is mortal” is a classic case of deductive reasoning. It’s often used in mathematical theorems and puzzles.

Structure of Deductive Arguments

Deductive arguments start with a general rule called a premise and reach a specific conclusion. Validity and soundness are essential in deductive reasoning. A valid argument means the conclusion must also be true if the premises are true. Soundness goes further, requiring the argument to be valid and the premises to be true.

The components of a deductive argument are the premise, which provides the general rule, and the conclusion, which is the specific outcome based on that rule. Deductive reasoning relies on the principle that if the premises are true, the conclusion must also be true, without a doubt.

Validity and Soundness

Validity means being able to prove an argument as true. Soundness means the argument is valid and based on well-founded reasoning.

In deductive reasoning, validity is determined by whether the conclusion logically follows from the premises, not depending on their truth values. Soundness requires both validity and true premises.

In inductive reasoning, validity and soundness depend on whether the conclusion logically follows from true premises.

Abductive reasoning involves using existing knowledge to assess possibilities and deduce the most likely outcome.

Famous Examples: Mathematical Theorems

Mathematical theorems have greatly influenced the field of mathematics. One example is Pythagoras’ theorem, which explains the relationship between the sides of a right-angled triangle. Another famous theorem is Fermat’s Last Theorem, which remained unsolved for over 300 years.

These theorems expanded our understanding of mathematics and had practical applications in fields like physics, engineering, and computer science. They form the basis for developing mathematical principles, algorithms, and technologies in various industries today.

Their impact extends to ensuring the structural integrity of buildings and securing data in cybersecurity. Mathematical theorems continue to influence advancements across disciplines.

Inductive Reasoning Unveiled

Definition of Inductive Reasoning

Inductive reasoning is a logical process. It involves making generalizations based on specific observations.

For example, if someone observes that every cat they have ever seen has a tail, they may generalize that all cats have tails.

This method relies on creating patterns based on evidence and drawing a probable but not definite conclusion.

Inductive inferences are characterized by their probabilistic nature, as opposed to the certainty of deductive reasoning.

This method allows for an increase in human knowledge and aids in making predictions about future events.

In the scientific method, inductive reasoning is often used to form hypotheses based on observations.

Scientists gather specific data and then make generalizations about the natural world.

This process eventually leads to the formation and testing of scientific theories, making inductive reasoning an important part of the scientific process.

Characteristics of Inductive Inferences

Inductive inferences start with specific observations and lead to a generalized but not certain conclusion. For instance, seeing several red apples may lead to the generalized idea that all apples are red.

These inductive arguments help increase human knowledge and make predictions about future events. For example, observing individual birds’ behavior may lead to the generalization that birds of that species migrate at specific times.

The scientific method uses inductive reasoning. It collects data through observation and experiments and then forms a generalized conclusion. For instance, observing that adding a certain chemical to a plant makes it grow faster may conclude that the chemical promotes plant growth.

Strength of Inductive Arguments

Inductive arguments are evaluated based on the relevance of the evidence to the conclusion, the size of the sample, and its representativeness. A larger and more representative sample increases the likelihood that the conclusion is true.

In the scientific method, inductive reasoning supports claims by accumulating data, observing patterns, and formulating general principles based on specific instances. For example, when scientists observe repeated patterns in experimental results, they can make generalized conclusions about the behavior of certain phenomena.

Scientific Method as Inductive Reasoning

The scientific method involves inductive reasoning. It starts with specific observations and leads to a generalized conclusion that is likely but not certain. This type of reasoning allows for increased human knowledge and the ability to predict future events.

The scientific method uses inductive reasoning to make discoveries. It gathers data through observation and experimentation and uses that data to form a generalized conclusion. This allows scientists to draw inferences from their observations, leading to new discoveries and a better understanding of the natural world.

For example, scientists observe a reaction every time they mix two chemicals. From this observation, they could generalize that mixing those two chemicals always leads to a reaction. This inductive inference can then be used to predict the outcome of future chemical reactions.

Abductive Reasoning: Making Educated Guesses

Definition of Abductive Reasoning

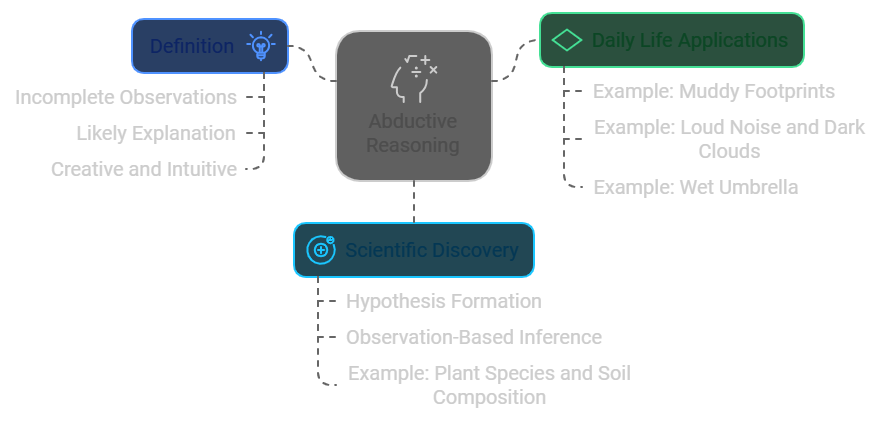
Abductive reasoning starts with incomplete observations and arrives at the likeliest possible explanation. A lack of completeness characterizes it, and it can be creative and intuitive.

In daily life, abductive reasoning is applied when someone finds clues and infers the likeliest explanation. For example, when a person finds muddy footprints in the house and deduces that someone must have walked in with dirty shoes.

In scientific discovery, abductive reasoning is used to form hypotheses, create new theories, and draw inferences based on observation. For instance, scientists make observations and then develop a hypothesis to explain them.

This method is not as certain as deductive or inductive reasoning, but it plays a crucial role in forming ideas and theories.

Abductive Reasoning in Daily Life

Abductive reasoning can help with everyday decision-making and problem-solving. It uses incomplete observations to arrive at the likeliest possible explanation.

For example, if someone hears a loud noise outside and sees dark clouds, they might reason that it will likely rain.

This method allows people to make educated guesses in daily life situations using incomplete information to arrive at the most probable conclusion.

For instance, if a person finds a wet umbrella by the door, they can reason that it likely rained while they were out.

In scientific discovery, abductive reasoning allows researchers to form initial hypotheses based on incomplete information.

It sets the stage for further investigation and experimentation to test the hypothesis and lead to discoveries.

Thus, abductive reasoning is a valuable tool for making decisions, solving problems, and advancing scientific knowledge.

Use in Scientific Discovery

Abductive reasoning is used in scientific discovery to arrive at the likeliest possible explanation based on incomplete observations.

For example, suppose a scientist observes that a certain plant species is thriving in a particular region but struggling in an adjacent region. In that case, they might use abductive reasoning to hypothesize that the difference in soil composition is the cause of the disparity.

Analogical reasoning is important in scientific discovery as it helps scientists draw parallels between different phenomena and apply knowledge gained from one area to another. For instance, a researcher studying the behavior of chimpanzees might use analogical reasoning to draw parallels between their behavior and that of early humans. This type of reasoning can help in the formulation of hypotheses and the generation of new knowledge.

Analogical Reasoning: Understanding Through Similarities

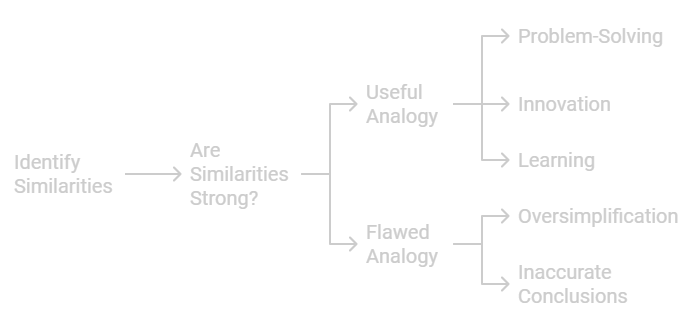
Definition of Analogical Reasoning

Analogical reasoning involves comparing two things that are alike in some ways but different in others. It’s used for problem-solving, innovation, and learning. Engineers use it to solve problems with new products by comparing them to similar ones they’ve designed before, and students use it to transfer knowledge from one concept to another.

One limitation is that analogies can sometimes lead to wrong conclusions if the similarities aren’t as strong as they seem. It can also be hard to figure out which aspects are relevant. Despite these issues, analogy connects concepts and creates new insights and solutions.

Analogies in Innovation and Learning

Analogies are important for learning and innovation. They help people understand new or complex ideas by using familiar concepts. For example, comparing the human brain to a computer can help us understand how the brain works.

Analogies also spark new ideas by encouraging creative thinking and applying concepts from different areas. However, it’s important to use analogies carefully. Misusing them can lead to faulty reasoning and an incomplete understanding of new ideas. For instance, comparing the brain to a computer may oversimplify the brain’s complexity.

So, while analogies can be helpful for learning and innovation, it’s essential to use them thoughtfully and critically. This ensures accurate and meaningful connections between ideas.

Strength and Limitations of Analogies

Analogies simplify complex ideas into relatable comparisons, making arguments easier to understand. They draw parallels between known and unknown concepts to increase human knowledge, like inductive reasoning.

For instance, comparing the human brain to a computer can help people grasp how memory works. However, analogies can oversimplify complex topics and lead to flawed conclusions.

They are similar to abductive reasoning, starting with incomplete observations, which can result in inaccurate or misleading conclusions.

An analogy comparing a company to a household budget may not cover all the financial operations a complex organization has to consider, potentially leading to erroneous decision-making.