Integration is something we experience every day. It’s in our meals’ delicious mix of flavors and the connected systems in our smartphones. Integration is essential in our lives.

In this article, we’ll look at the four types of integration simply. Whether you love technology and food or want to understand how things work, this article will give you insights into the different types of integration that shape our world.

What is Integration?

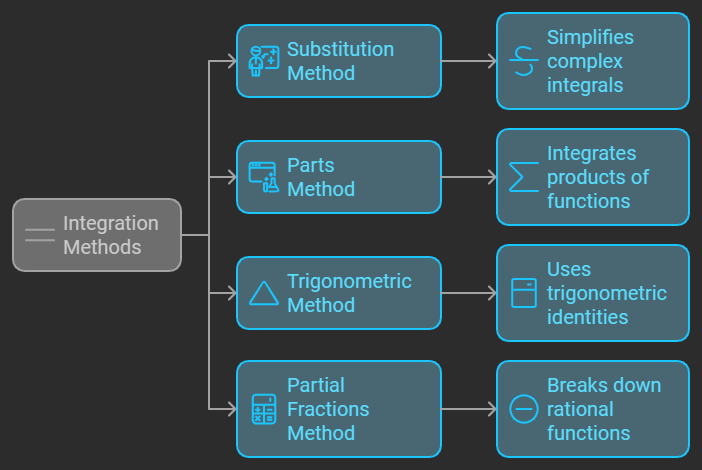
Four different methods are used in math integration: the substitution method and the parts method. These methods provide alternative ways to find a function’s integral, making it easier to evaluate the original integral.

Integration by substitution involves introducing a new independent variable to simplify a function’s integral. Integration by parts is a technique for integrating a function that is the product of two or more functions.

Integrating using trigonometric identities involves simplifying trigonometric functions in integrals. Integration by partial fraction deals with expressing a rational function as the ratio of two polynomials, which can be expressed as partial fractions.

These methods make integrating functions in math more manageable and are widely used in various mathematical applications.

For example, in business, horizontal integration involves a company acquiring or merging with a similar company in the same industry. Vertical integration is the expansion of a business within the same production path, such as a manufacturer acquiring its supplier or distributor.

Understanding Math Integration

Substitution Method

The substitution method makes solving complex integration problems easier. It introduces a new independent variable, usually t, instead of x. By transforming the original integral function, the process becomes simpler.

The steps for using the substitution method are:

1. Identify the integral function.
2. Introduce a new independent variable, t, by substituting x.
3. Transform the integral function into a new form for easier evaluation.

This method simplifies the integration of complex expressions, especially those involving multiple functions or trigonometric identities. It makes the original integral function more manageable and easier to evaluate and solve.

Parts Method

The Parts Method is a math integration technique. It helps integrate a function that is the product of two or more functions. This method uses the representation? f(x)·g(x)·dx = f(x)·?g(x)·dx – ?(f'(x)·?g(x)·dx)·dx. It follows the ILATE rule to decide the first and second functions.

Compared to the Substitution and Trigonometric Methods, the Parts Method is especially useful for integrand functions that result from multiplication. It is essential for dealing with integrals of products of functions, and it can solve definite integrals and problems involving repeated application.

The Parts Method has practical applications in problem-solving in various areas, such as mathematical physics, probability, fluid dynamics, economics, and engineering. For example, it can be used in economic models involving multiple interacting factors and in physics problems requiring the integration of functions’ products.

Using the Parts Method makes it easier to evaluate the original integral. This enables the analysis and interpretation of complex functions through multiple mathematical approaches.

Trigonometric Method

The trigonometric method makes integration easier by using trigonometric identities to simplify functions. This is especially helpful for integrating functions involving trigonometric functions. It offers a different approach than substitution, integration by parts, and integration by partial fractions.

Unlike other methods involving different mathematical manipulations, the trigonometric method focuses specifically on working with trigonometric identities to simplify integrands and find integrals.

In real-world applications, the trigonometric method is practical for precise measurements and calculations. For example, engineering is essential for accurately modeling and analyzing waveforms, sound, and mechanical motion. It is also widely used in physics, astronomy, and navigation, showing its broad real-world relevance beyond mathematical abstractions.

Partial Fractions Method

The Partial Fractions Method is a technique used in mathematical integration. It breaks a rational function into simpler fractions. This method is helpful for complex rational functions that are hard to integrate using other methods.

To use the Partial Fractions Method, follow these steps:

1. Factor the given rational function into irreducible factors.
2. Use the method of equating coefficients to find the coefficients of the unknown fractions.
3. Once you have the values of the unknown fractions, split the original rational function into these simpler fractions for easier integration.

When comparing the Partial Fractions Method to other integration methods like Substitution, Parts, and Trigonometric methods, the key difference is the types of functions they are best suited to integrate. Each technique serves a unique purpose in simplifying and incorporating different types of functions:

• The Partial Fractions Method works with rational functions.
• The substitution method works with algebraic functions.
• The parts method is ideal for products of functions.
• The trigonometric method is beneficial for trigonometric functions.

Getting to Know Business Integration

Horizontal Integration Explained

Horizontal integration occurs when a company merges with or acquires a similar company to strengthen its market position or expand its activities within the same industry. This allows the company to benefit from cost savings, increased market share, and economies of scale. It differs from vertical integration, which involves purchasing suppliers or distributors.

A well-known instance of horizontal integration is Facebook’s 2012 acquisition of Instagram, which enabled Facebook to grow its user base and services. Another example is the Walt Disney Company acquiring 21st Century Fox, which expanded its content creation and distribution abilities. These real-world cases show how horizontal integration can lead to strategic advantages and greater market dominance.

What’s Vertical Integration?

Vertical integration in business means merging or acquiring companies at different supply chain levels. It combines businesses producing goods or services at various production stages. This lets the business control more of the supply chain, from raw materials to the final product, for better oversight and efficiency. It can streamline the supply chain and production, leading to cost savings and quality control.

However, it can also increase complexity and risk in managing a larger, diverse business. Despite this, many companies have used vertical integration to strengthen their competitive advantage and gain market control.

Comparing Horizontal and Vertical Integration

The Benefits

Horizontal integration in a business has many benefits. It can increase market share and reduce competition. When companies merge or acquire similar businesses, they can expand their customer base, increase overall sales, and have a more substantial presence in the market.

For example, a fast-food company that acquires another fast-food chain can benefit from additional locations and eliminate a direct competitor.

Vertical integration gives companies advantages like cost savings and increased control over the supply chain. By acquiring suppliers or distributors, companies can reduce costs, improve efficiency, and have more control over the quality of their products.

In mathematics, integration methods can help solve complex problems. They provide different approaches to finding areas under curves and solving differential equations.

For instance, the method of integration by parts allows mathematicians to solve integrals of products of functions, which might not be easily solved using basic integration techniques.

The Drawbacks

The substitution method in math integration can be tricky. Sometimes, it’s hard to find a function’s integration. This method involves introducing a new independent variable, which can be complex. Transforming the integral function into another by changing the independent variable may not be straightforward.

Similarly, the parts method for mathematical integration has its drawbacks. This special technique for integrating a function where the integrand function is the multiple of two or more functions requires careful consideration. We need to decide the first and second functions based on specific rules.

Implementing horizontal integration can also have drawbacks in a business context. It can lead to challenges related to cultural differences, overlapping responsibilities, and possible resistance from employees. Therefore, it is important for businesses to carefully strategize and navigate potential drawbacks.

Real World Examples

Famous Horizontal Integration Cases

Many prominent companies, including those in the technology, media, and oil industries, have successfully utilized horizontal integration throughout history.

For example, in the technology sector, notable cases of horizontal integration have involved the acquisition of smaller tech startups by industry giants. Similarly, media conglomerates have expanded their market share and influence through horizontal integration by acquiring other media companies and increasing control over various media forms (e.g., print, television, digital). In the oil industry, companies have employed horizontal integration strategies to merge with or acquire their competitors, resulting in a more consolidated and powerful presence within the market. These cases of horizontal integration have significantly impacted their respective industries and the broader economy, often leading to increased market concentration, reduced competition, and significant changes in consumer choices and prices.

Famous Vertical Integration Cases

Vertical integration is when businesses control various stages of the production process, from raw materials to final sales, under one ownership. Famous examples include the Ford Motor Company, Andrew Carnegie’s steel business, and the oil giant Standard Oil.

For Ford, this meant taking over companies that produced steel, glass, and tires, streamlining operations, and reducing costs. Standard Oil effectively monopolized the oil industry and controlled all aspects of production, from drilling to distribution.

While vertical integration increased efficiency and lowered costs, it also faced criticism for creating unfair market advantages and stifling competition. Advantages included increased control over the supply chain, ensuring consistent product quality, and reducing reliance on external suppliers. However, there were also disadvantages, such as the potential for anti-competitive behavior and the significant investment required to establish and maintain integrated operations.